Next: Other Forces Affecting Deceleration
Up: Braking
Previous: Braking
To simplify matters for the moment, we will
assume constant deceleration and ignore the contribution of wind resistance. We
will also, for the moment, pretend that braking traction is independent of
cornering traction. In reality, if the car is at
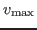 , all of its traction is
used up keeping it from sliding sideways; no traction would be available for
braking.
, all of its traction is
used up keeping it from sliding sideways; no traction would be available for
braking.
The equations for position and velocity as a function of time under constant
acceleration are
Since we're describing braking, the number that we plug in for 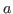 will be a
negative number. To get
will be a
negative number. To get  we note that
we note that
 and
that
and
that
 . Substituting and solving gives
. Substituting and solving gives
 |
(23) |
Here,  is the position of the car when braking starts. For the remainder
of the discussion we will set
is the position of the car when braking starts. For the remainder
of the discussion we will set 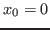 and interpret
and interpret 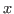 as the distance
traveled since braking started. The initial speed
as the distance
traveled since braking started. The initial speed 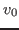 is the car's speed when
braking started. Our final drag-free braking equation is
is the car's speed when
braking started. Our final drag-free braking equation is
 |
(24) |
Equation 24 defines the boundary between reachable and
unreachable points in the 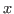 -
-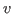 graph for track positions ahead. This
boundary curve must not exceed
graph for track positions ahead. This
boundary curve must not exceed
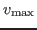 or the car will slide off the road. We
can ensure that it does not by checking the curve during each timestep in the
simulation. If the curve touches
or the car will slide off the road. We
can ensure that it does not by checking the curve during each timestep in the
simulation. If the curve touches
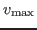 it's time to brake.
Figure 8 illustrates the process.
it's time to brake.
Figure 8 illustrates the process.
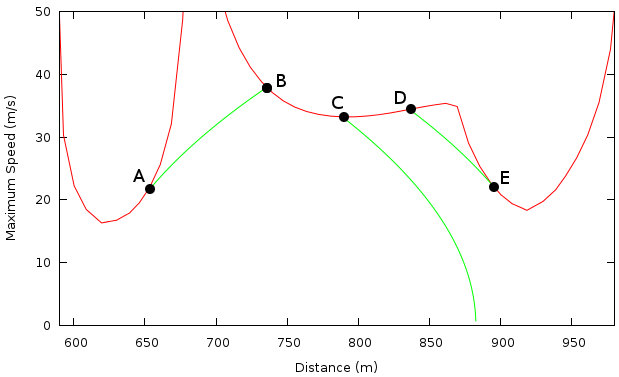
Figure 8:
Optimal speed through turns 4, 5, and 6 for a car that can accelerate
and brake at 0.6g. At the exit of turn 4 (point A) the car undergoes
maximum acceleration until it reaches
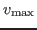 in turn 5. At point C, the
braking curve stays below
in turn 5. At point C, the
braking curve stays below
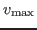 , so the car maintains
, so the car maintains
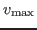 . Braking begins
at point D to avoid exceeding
. Braking begins
at point D to avoid exceeding
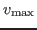 in turn 6. Braking ends at point E.
From here the car maintains
in turn 6. Braking ends at point E.
From here the car maintains
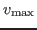 until it can accelerate at the exit of
turn 6.
until it can accelerate at the exit of
turn 6.
|
|



Next: Other Forces Affecting Deceleration
Up: Braking
Previous: Braking
Sam Varner
2012-01-18


![]() -
-![]() graph for track positions ahead. This
boundary curve must not exceed
graph for track positions ahead. This
boundary curve must not exceed
![]() or the car will slide off the road. We
can ensure that it does not by checking the curve during each timestep in the
simulation. If the curve touches
or the car will slide off the road. We
can ensure that it does not by checking the curve during each timestep in the
simulation. If the curve touches
![]() it's time to brake.
Figure 8 illustrates the process.
it's time to brake.
Figure 8 illustrates the process.