Steering

The racing line tells where to go, the robot just needs to turn the steering wheel to keep the car centered on the line. However, simply setting the steering angle in proportion to distance between the car's centerline and the racing line does not work well. Changing the steering angle does not immediately affect its lateral position. The car travels in an arc that's tangent to its previous path. The old path and new path diverge slowly at first as shown in figure 4.

Figure 4: After the steering angle changes from zero to non-zero, the car's new path deviates from its old path slowly at first.

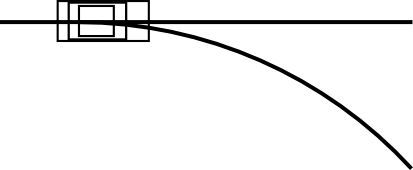
This delay between setting the steering angle and appearance of its desired effect inevitably leads to oscillation. The change in steering angle doesn't immediately change what we're trying to control--the lateral position of the car--so the robot changes it some more. Eventually it finds itself quickly traveling across the desired position so it starts steering in the opposite direction.

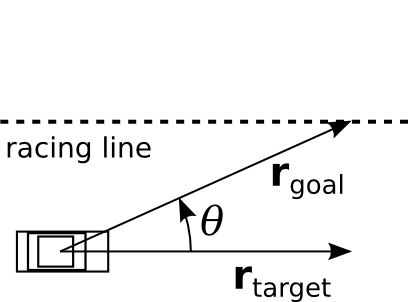
Control becomes much more stable if we aim for a point farther down the road. Imagine a long pole extending in front of the car. Instead of trying to keep the car on the line, we try to keep the tip of the pole on the line. More precisely, if we define $\ensuremath {\mathbf {r}_{\mathrm {target}}}$ to be the vector from the center of the car to the tip of our pole, and $\ensuremath {\mathbf {r}_{\mathrm {goal}}}$ to be the vector from the center of the car to a point ahead of the car on the racing line, then we can use the angle between them as the steering angle.

$$\sin \theta = (\ensuremath{\mathbf{r}_{\mathrm{target}}} \times \ensuremath{\m... ...hbf{r}_{\mathrm{target}}}\vert\vert\ensuremath{\mathbf{r}_{\mathrm{goal}}}\vert$$ (13)

$$\theta \approx (\ensuremath{\mathbf{r}_{\mathrm{target}}} \times \ensuremath{\mathbf{r}_{\mathrm{goal}}}) \cdot \mathbf{z}$$ (14)

Figure 5: The steering angle is determined from $\ensuremath {\mathbf {r}_{\mathrm {goal}}}$, which points straight ahead, and $\ensuremath {\mathbf {r}_{\mathrm {target}}}$ which points to the racing line.