
|
As an example, take a look at the track in figure 1. If you were trying to set a fast lap time, you would stick to the right-hand side of the road down the long straight and make a smooth curve through the first two left turns. You would cross the track to set up for the right-hand turn 3. This turn is followed closely by the sharp left-hand turn 4, so you can't take the ideal line through both; you need to compromise the exit of 3 to make a decent entrance to 4. After that you sweep through 5 and set up to make the widest possible curve through turn 6 so that you carry as much speed as possible down the long straight.
From this exercise it seems that a good racing line is one that minimizes curvature. We can find a path that minimizes curvature by simulating a chain of masses on spring-loaded hinges that loops around the track and connects to itself. We will start by placing the masses on the centerline of the track and constrain them to stay on the track surface. As we propagate the system forward in time, the springs will open the hinges and the masses will shift until we approach a smooth curve that minimizes the energy stored in the springs.
|
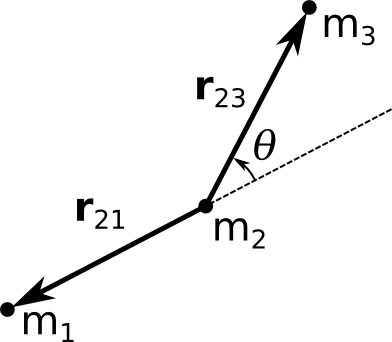
The force acting on a given mass ![]() can be calculated from the relative
positions of its neighbors as shown in figure 2.
Let's start by assuming that closing the hinge produces a torque proportional to
the angular displacement.
can be calculated from the relative
positions of its neighbors as shown in figure 2.
Let's start by assuming that closing the hinge produces a torque proportional to
the angular displacement.
| (1) |
We can calculate
![]() from the cross product of
from the cross product of
![]() and
and
![]() .
.
| (3) | |||
| (4) | |||
| (5) | |||
| (6) |
We can define the curvature vector ![]() at
at ![]() to be
to be
| (9) |
The forces are calculated for each contiguous triplet of nodes. The total force on a given node is the sum of the forces exerted by its neighbor's hinges, and the reaction forces from the force of its own hinge on its neighbors. Instead of allowing the nodes to move freely in all directions, we constrain the nodes to move across the track. This constraint improves stability which allows us to use higher hinge torques which in turn gives faster convergence. The node's motion is damped to improve stability.
Once the total force on each node is calculated a new position for the node is
calculated using Newton's laws of motion and the Euler method.
| (11) | |||
| (12) |
The curvature need not be calculated until propagation is finished, but equation 10 shows that it may be convenient to calculate curvature as the forces are calculated during propagation.

|
The racing line calculated for the example track shown in figure 3 matches well with what we would expect. However, there is still a little distortion around the sharp turn 4. The curve flattens out a bit after the apex.