


Next: Braking
Up: Speed Control
Previous: Speed Control
The centripetal acceleration can be calculated from the car's speed and
trajectory as 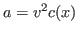 where
where  is the distance along the track and
is the distance along the track and
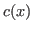 is the curvature of its path at that distance. If the car is driving on
the racing line, the curvature can be obtained as shown in
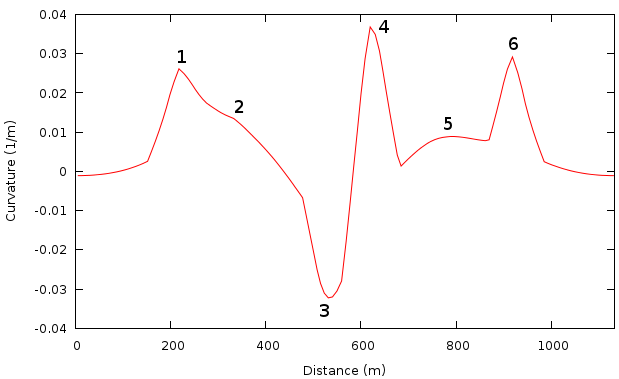
section 2. The curvature as a function of distance for
the example track (figure 1) is shown in
figure 6.
is the curvature of its path at that distance. If the car is driving on
the racing line, the curvature can be obtained as shown in
section 2. The curvature as a function of distance for
the example track (figure 1) is shown in
figure 6.
Figure 6:
Curvature of the racing line for the example track. Curvature peaks
near the turns. Curvature is positive for left turns.
|
|
Banking and elevation changes can affect the maximum safe speed for a corner.
If a corner is at the crest of a hill, the car will get light and lose some
traction. In general, gravity, normal, and frictional forces must sum to the
centripetal force. Forces normal to the road can be ignored, so we have
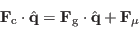 |
(15) |
where
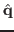 is the unit vector parallel to the road and away from the center
of curvature. The frictional force is
is the unit vector parallel to the road and away from the center
of curvature. The frictional force is
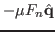 where
where 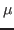 is the
coefficient of static friction and the normal force
given by
is the
coefficient of static friction and the normal force
given by
 |
(16) |
where 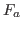 is aerodynamic downforce. We substitute the following expressions
for the forces
is aerodynamic downforce. We substitute the following expressions
for the forces
and solve for  .
.
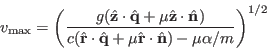 |
(20) |
The fastest way around the track is to stay as close as possible to
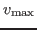 without going over. Figure 7 shows part the
without going over. Figure 7 shows part the
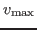 curve for the
example track.
curve for the
example track.
Figure 7:
Maximum speed on the example track's racing line for the a car capable
of 1g lateral acceleration.
|
|



Next: Braking
Up: Speed Control
Previous: Speed Control
Sam Varner
2012-01-18

![]() without going over. Figure 7 shows part the
without going over. Figure 7 shows part the
![]() curve for the
example track.
curve for the
example track.
